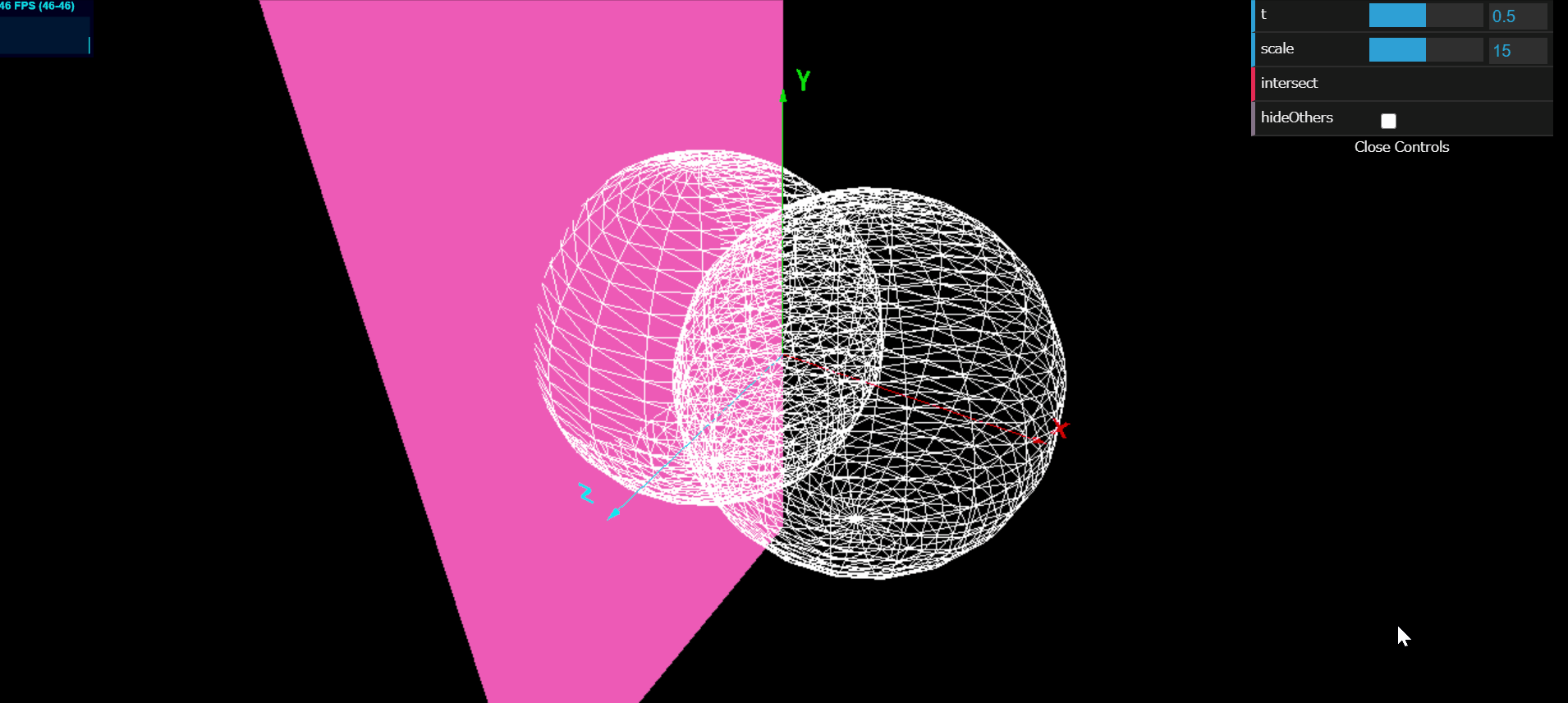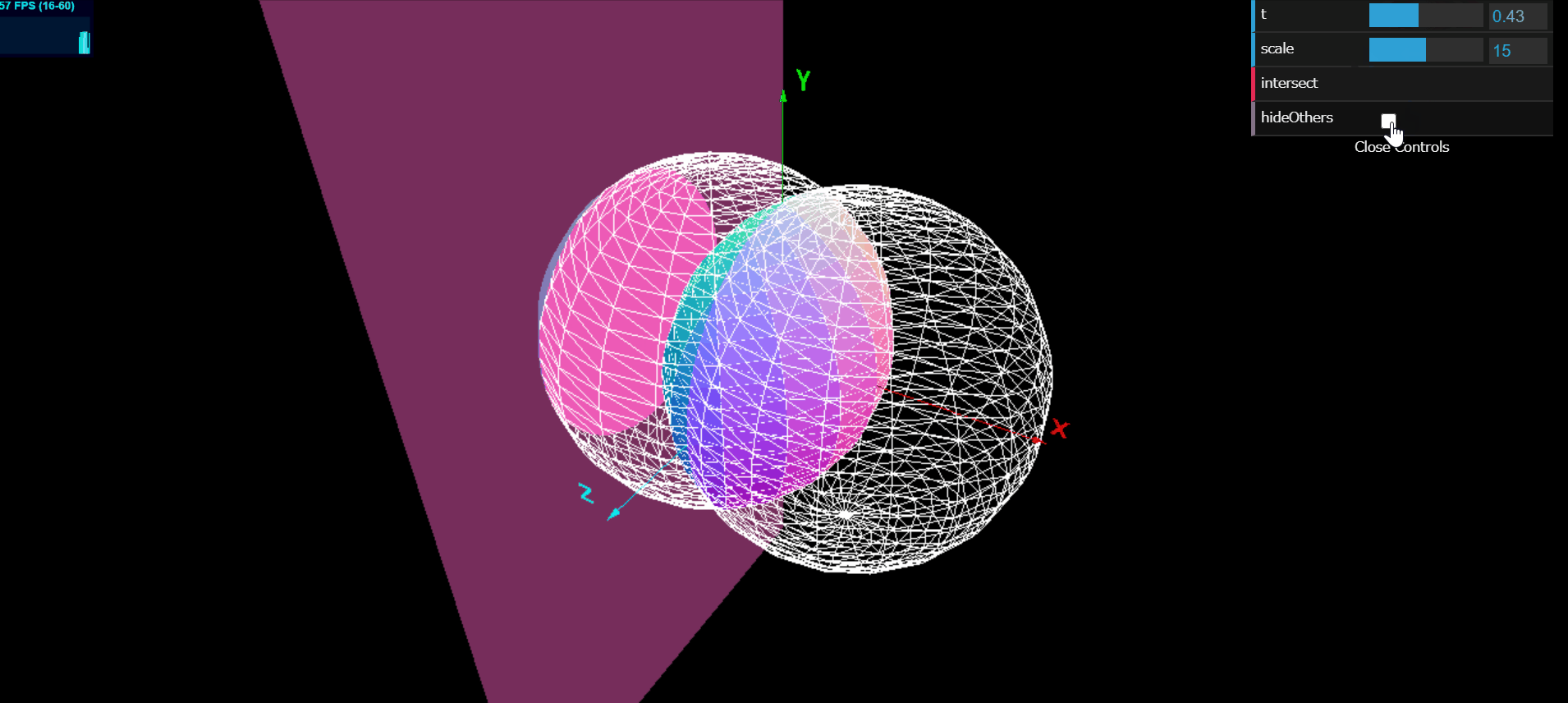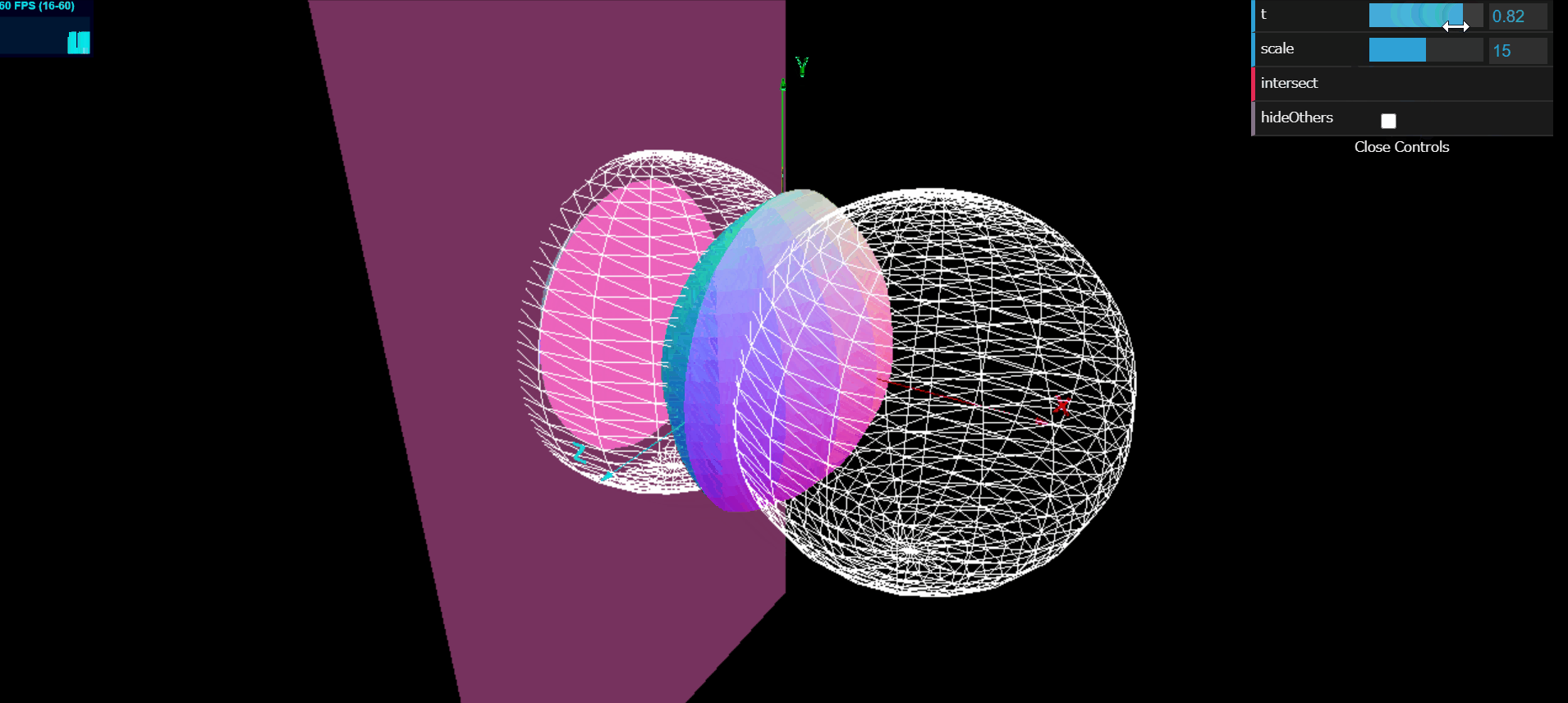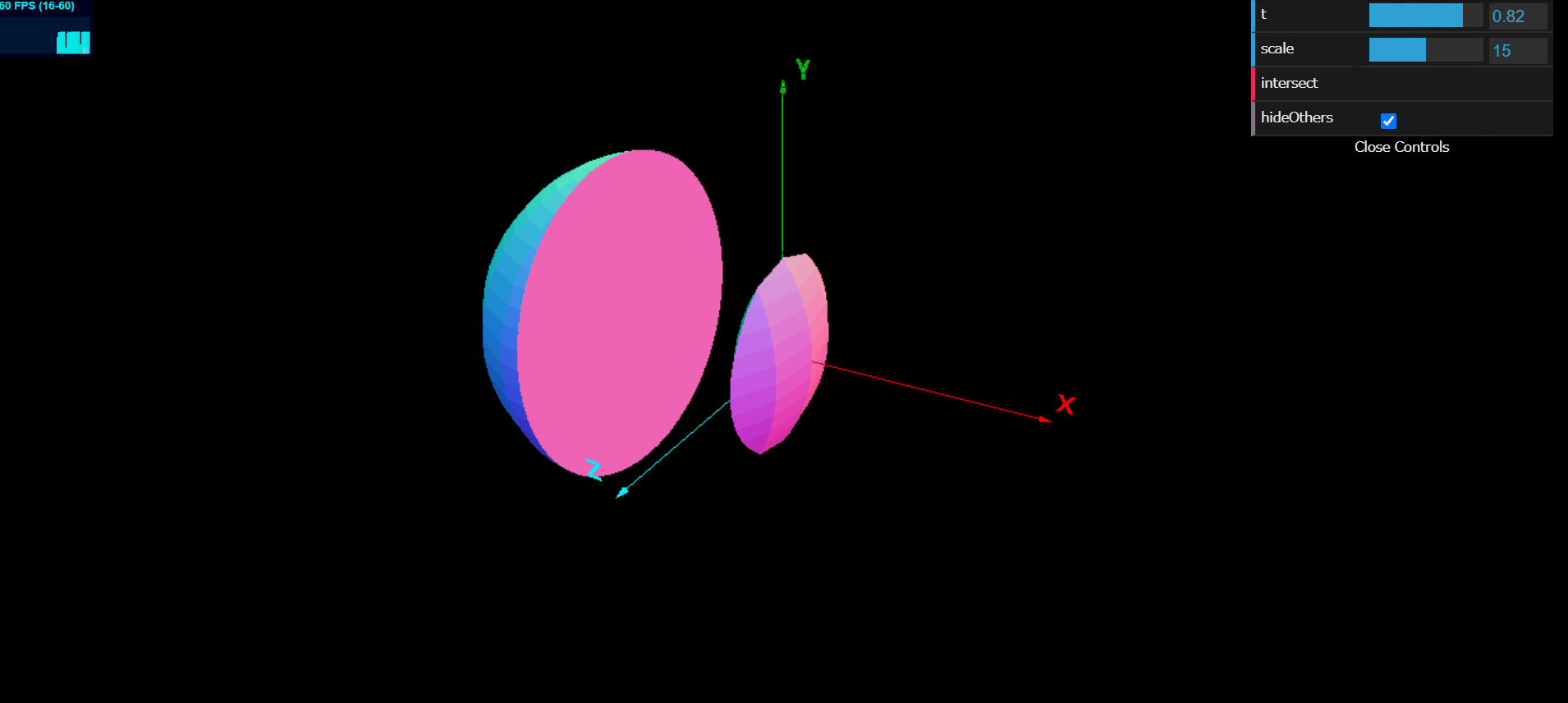$3$次関数 $y = x^3 - 2 x^2 - x + 2$ のグラフ上の点 $(1, 0)$ における接線を $l$ とする. この$3$次関数のグラフと接線 $l$ で囲まれた部分を $x$ 軸の回りに回転して立体を作る. その立体の体積を求めよ.

回転体は以下のようになります. phiLengthの値を調整することで, 回転体が形成される様子を見ることが出来ます. なお, 単位はラジアンです.
※アニメーションをクリックすると, 別タブが開き, 図形を操作することができます.

$r$ を正の実数とする. $xyz$ 空間内の原点 $O(0,0,0)$ を中心とする半径 $1$ の球を $A$, 点 $P(r, 0, 0)$ を中心とする半径 $1$ の球を $B$ とする. 球 $A$ と球 $B$ の和集合の体積を $V$ とする. ただし, 球 $A$ と球 $B$ の和集合とは, 球 $A$ または球 $B$ の少なくとも一方に含まれる点全体よりなる立体のことである.
(1) $V$ を $r$ の関数として表し, そのグラフの概形をかけ.
(2) $V = 8$ となるとき, $r$ の値はいくらか. 四捨五入して小数第1位まで求めよ.
注意：円周率 $\pi$ は $3.14 < \pi < 3.15$ をみたす.

以下は, 球 $A$ と 球 $B$ です. $r$ の値を変化させることで, 球 $B$ を移動させることができます. また, intersect を押すと, 二つの球の共通部分が得られます. (和集合の体積は, 二つの球の体積から共通部分の体積を引けば求められます.) hideWireframesにチェックを入れると, 球の表示を無くすことができます. ※アニメーションをクリックすると, 別タブが開き, 図形を操作することができます.

座標空間の $x$ 軸上に動点 $P$, $Q$ がある. $P$, $Q$ は時刻 $0$ において, 原点を出発する. $P$ は $x$ 軸の正の方向に, $Q$ は $x$ 軸の負の方向に, ともに速さ $1$ で動く. その後, ともに時刻 $1$ で停止する. 点 $P$, $Q$ を中心とする半径 $1$ の球をそれぞれ $A$, $B$ とし, 空間で $x \ge -1$ の部分を $C$ とする. このとき, 以下の問いに答えよ.
(1) 時刻 $t$ ($0 \le 1$) における立体 $(A \cup B) \cap C$ の体積 $V(t)$ を求めよ.
(2) $V(t))$ の最大値を求めよ.

以下は, $(A \cup B) \cap C$ を表した図です. $t$ の値が経過した時間に対応しています. intersect を押すと, 二つの球の共通部分と $A$ と ($C$ の補集合) の共通部分が得られます. (和集合の体積は, 二つの球の体積からこれらの体積を引けば求められます.) hideOthersにチェックを入れると, 球と平面の表示を無くすことができます. ※アニメーションをクリックすると, 別タブが開き, 図形を操作することができます.